La une est la première page d’un journal. Sur la première page d’un journal, on voit le ventre, l’oreille, le pied de page, la tribune, la manchette, le bandeau et la rivière d’appelle (serie d’informations courtes qui forment une colonne).En premier nous avons regardé plusieurs unes. Ensuite nous avons comparé les unes de plusieurs journaux du jour.
Auteur : Oriane
Cliquez sur les titres colorés
|
||
|
|
Les sources d’information |
|
Les Unes des journaux |
 |
Écrire des articles à la manière des journalistes |
Twitter, qu’est-ce que c’est ? |
||
Nous pouvons être informés par des journaux papier, la télévision, les radio, internet, les réseaux sociaux comme Twitter.
Nous avons appris à écrire un message sur Twitter :
Notre compte Twitter est @MEtigny pour « les moineux d’Etigny ». Nous avons twitté nos premiers messages à des journalistes de plusieurs média (journaux papier, journaux télévisés, radio) pour rechercher des journalistes et leur poser des questions.
Auteur : Maram (CE2)
Nous sommes allés au collège pour la semaine des maths. Nous avons réalisé quelques activités. L’une d’entre elles était « la roue de vélo ». Il fallait représenter le trajet dans l’espace d’un chewing-gum collé sur la roue et voici les dessins que nous avons réalisés :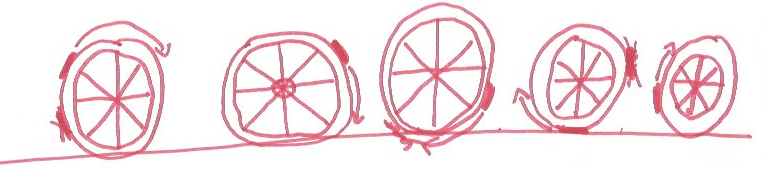
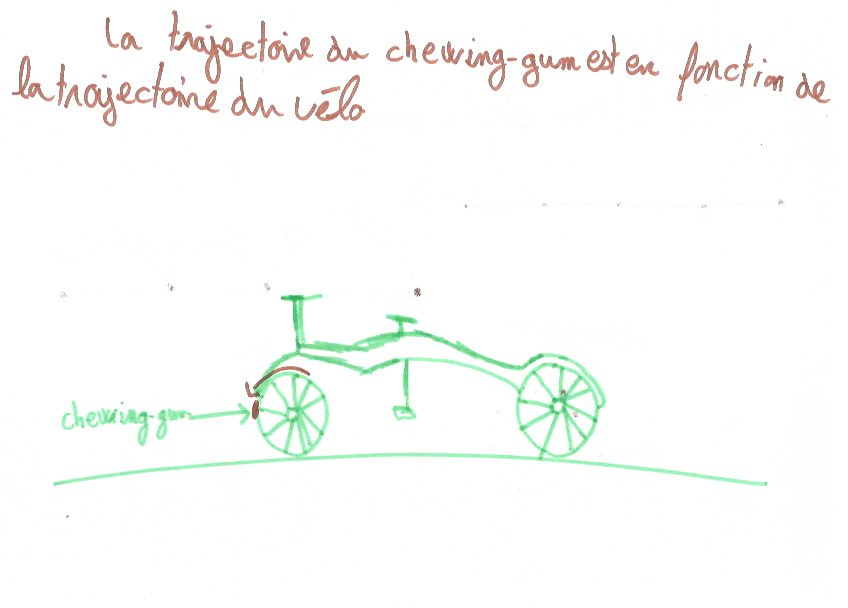
Pour dessiner la trajectoire, nous avons eu plus de difficulté (voir la vidéo ici).
Mais finalement, en faisant rouler une roue de vélo sur laquelle était collé un repère en scotch, nous avons tous compris que la trajectoire du chewing-gum ressemble à cela :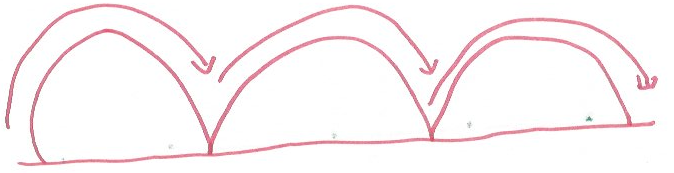
On appelle cette trajectoire une cycloïde.
Ensuite il fallait essayer de voir ce que ça ferait, si le chewing-gum laissait des taches d’encre et voici comment nous avons schématisé ces traces :
À partir d’une certaine roue (petite, moyenne ou grande), sans faire rouler la roue au sol, il fallait calculer les emplacements exacts des empreintes de chewing-gum sur la route.
Comme nous n’avons pas eu le temps de finir ces calculs au collège, nous les avons repris à l’école.
Au départ, nous nous sommes dit qu’il fallait calculer la longueur d’un demi- cercle en reprenant la trajectoire du chewing-gum dans l’espace.
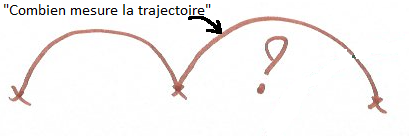
Mais en traçant plusieurs cycloïdes dans la classe avec des objets différents, nous avons vu qu’il n’y a pas de demi-cercles dans une cycloïde mais des arcs de cercle plus ou moins grands !
Matériel utilisé pour tracer les cycloïdes :
Agnès nous a dit de réfléchir encore à ce que nous devions calculer et d’écrire ce que nous savions :
Avec ces phrases, nous nous sommes rendu compte que l’espace entre deux empreintes correspond à la « longueur d’une roue dépliée », c’est-à-dire au périmètre du cercle, à la circonférence de la roue.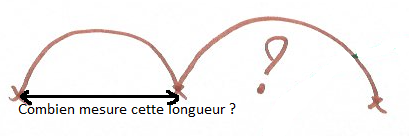 
Pour connaitre cette circonférence, il faut faire la formule :
∅ × 3,14 ou R × 2 ×3,14
Matys et Maxime ont pris une règle et mesuré le diamètre de la roue du vélo. Le calcul donne un résultat de 188 cm. Ils ont tracé les empreintes du chewing-gum sur une bande de papier :
Auteurs : Axel et Matys (CM2)
Il y a plusieurs ballons de foot différents. Tous les quatre ans, il existe un nouveau ballon de coupe du monde.
Les anciens ballons sont faits à partir de pentagones et d’hexagones. Pour le patron, il faut avoir 20 hexagones et 12 pentagones et il ne faut pas que de pentagones se touchent.
Nous avons observé sur le Brazuca (le ballon de foot de la coupe du monde 2014) qu ‘il n’était pas constitué de pentagones et d’hexagones.
Les constructeurs du ballon ont eu l’idée d’un ballon composé de la même forme mais qui se répète six fois, comme un cube (voir article du mathématicien Etienne Ghys) !
Le patron du Brazuca est donc très différent : il contient beaucoup moins d’éléments qui sont tous de la même forme . Voici son patron d’assemblage :
Pour construire notre ballon nous avons construit une forme (voir ici). Il fallait 6 fois cette forme :
et les assembler en respectant la matrice du Brazuca.
Voici un assemblage :
Dans une deuxième étape, nous allons réfléchir à la forme qu’il faudrait pour combler les trous. Nous sommes quand même fiers de notre ballon ! Pour l’instant le nom de notre prototype est l’ÉTITROUS !
Auteurs : Émilie et Baptiste pour le texte et les photos, Coraline pour la maquette.
Si on lance un ballon de basket, on obtient une trajectoire qui sera en forme de parabole. Une parabole est une courbe qui a comme particularité qu’au point le plus haut de la trajectoire (entre la montée et la descente du ballon) les deux parties de la courbe sont symétriques.
Si on lance un volant de badminton, on obtient une trajectoire différente. Elle commence une courbe et à partir du point le plus haut redescend en parcourant moins de distance.
Expliquer la différence de trajectoire :
Auteur : Arthus (CM1)
Avec la puissance que nous donnons quand nous tapons dans le volant de badminton, le poids du volant étant lourd, il s’écrase et la trajectoire fait cela :
Auteur : Théo (CM2)
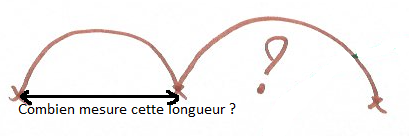
Chronophotographie de la trajectoire d’un volant de badminton réalisée à partir du film que nous avons pris en décembre 2015 lors de notre première visite au collège. La chronophotographie a été faite par M. Dumont.
On peut voir sur cette image que la trajectoire de part et d’autre de la droite rouge (perpendiculaire au sol et qui passe par le point le plus haut du volant) n’est pas identique. à partir de ce point, le volant en retombant aura parcouru moins de distance que dans sa trajectoire ascendante. La courbe n’est pas une parabole.
Le 16 mars 2016, à l’occasion de la semaine des mathématiques, nous nous sommes rendus au collège Chateaubriand de Villeneuve/Yonne pour faire des ateliers « Maths et sport » avec une classe de sixième.
Trois ateliers étaient à parcourir :
Notre projet était de travailler sur la chronophotographie (voir dans cet article , celui-ci , celui-là et le suivant comment nous avions déjà abordé le sujet). Nous connaissions déjà un peu le collège pour y avoir filmé la même classe lors d’une séance d’EPS (badminton) en décembre 2015.
Voici un petit résumé filmé de notre journée de mercredi :
Les CE2 vous racontent leurs impressions :
Récit d’Enora
La première fois que nous sommes allés au collège il y avait la moitié des collégiens qui étaient autour de nous. Il y avait des élèves d’Etigny qui avaient peur et d’autres non. La première fois qu’on y est allés, c’était pour filmer des collégiens en train de faire du sport pour après pouvoir étudier la trajectoire du volant. La deuxième fois, c’était pour la semaine des mathématiques. Il avait trois groupes et trois ateliers : un sur la trajectoire du volant et du ballon de Basket qui était avec M. Dumont. Le deuxième atelier c’était avec Mme Toubiana : on devait faire le dernier ballon de la coupe du monde avec ses six formes. Le troisième c’était avec Agnès, on travaillait sur le cyclisme. Après nous avons pris le car pour rentrer à l’école.
Récit de Marie-Noëlle
Au collège on a appris beaucoup de choses. La première chose qu’on avait à faire était d’imaginer la trajectoire d’un chewing-gum dans l’espace. La deuxième chose à faire était de la technologie avec M. Dumont en traçant la trajectoire d’un ballon de basket et d’un volant. La troisième chose était de faire un ballon en carton et de le décorer.
Voici le modèle pour le ballon à partir du Brazuca :
Récit d’Oriane
Quand nous avons fait notre première sortie au collège, moi j’étais timide, certains n’avaient pas du tout peur. On se serrait tous. Tous les collégiens nous regardaient. Il y en avait qui ne nous quittaient pas des yeux. Quand nous sommes rentrés dans la salle de sport, nous avons soufflé. Pendant les explications, beaucoup de collégiens nous regardaient encore.
Mercredi 16 mars 2016, nous sommes retournés au collège. Je n’étais plus du tout timide. Nous avons fait des maths avec Agnès et Mme Toubiana. Nous avons fait de la technologie avec M. Dumont. Au moment de la récréation, certains jouaient et d’autres se parlaient dans un coin.
Trajet parcouru de l’école au collège
Récit d’Elsa
La première fois que nous sommes allés au collège nous étions tous collés à Agnès car on avait un peu peur ! Tous les collégiens étaient autour de nous. Moi j’avais peur mais pas trop à la fois parce qu’il y avait mes sœurs. Mercredi 16 mars 2016, quand nous sommes arrivés au collège, il n’y avait personne dans la cour parce que les élèves étaient en cours. Après nous nous sommes mis en groupe pour faire des mathématiques car c’était la Semaine des maths. Puis mon groupe et moi, nous sommes allés avec Agnès. Nous avons changé de salle tous les trois quarts d’heure pour être avec d’autres professeurs : M. Dumont et Mme Toubiana.
Trajet parcouru pour se rendre de l’école au collège
L’histoire de l’aviation montre que depuis très longtemps (au moins depuis l’Antiquité), l’homme a le désir de quitter la terre pour voler.
Au fil des événements qui sont listés ici, on voit que le vol aérien n’a pas toujours été au service de l’aventure : comme toutes les machines, les avions peuvent être utilisés dans les conflits et apporter la mort (voir l’article Guernica).
L’ A380 est le plus gros avion de transport de personnes du monde. Il mesure du bout de l’aile à l’autre près de 80 m. Il peut transporter 550 passagers et même 880 dans les versions futures. Pour que l’avion soit plus léger, il a été construit en partie en carbone. Ses 4 réacteurs ont aussi été faits de façon à réduire le carburant nécessaire.
Auteurs : Coraline et Léandre
Guernica est une ville d’Espagne qui a été réduite en cendres le 26 avril 1937 pendant la guerre civile. Les bombardements ont été faits par de nouveaux avions utilisés pour la première fois pour faire la guerre. Ces avions sont allemands. Picasso est un peintre très célèbre. Il a peint Guernica.
Guernica de Picasso (peint du premier mai au 4 juin 1937) 
Picasso décrit l’horreur de la guerre. Il représente des corps dans tous les sens, démembrés. Une mère hurle de douleur en portant son enfant mort. Un cheval et un taureau, symboles de l’Espagne, apparaissent dans le tableau. Eux aussi sont victimes des bombardements.
Auteurs : Théo et Baptiste